Using BEN (simple_bdi)

Introduction to BEN

BEN (Behavior with Emotions and Norms) is an agent architecture providing social agents with cognition, emotions, emotional contagion, personality, social relations, and norms. This work has been done during the Ph.D. of Mathieu Bourgais, funded by the ANR ACTEUR.

The BEN architecture is accessible in GAMA through the use of the simple_bdi architecture when defining agents. This page indicates the theoretical running of BEN as well as the practical way it has been implemented in GAMA.

This page features all the descriptions for the running of the BEN architecture. This page is updated with the version of BEN implemented in GAMA. To get more details on its implementation in GAMA, see operators related to BDI, BDI tutorial or BDI built-in architecture reference.

The BEN architecture

The BEN Architecture used by agents to make a decision at each time step is represented by the image right below:

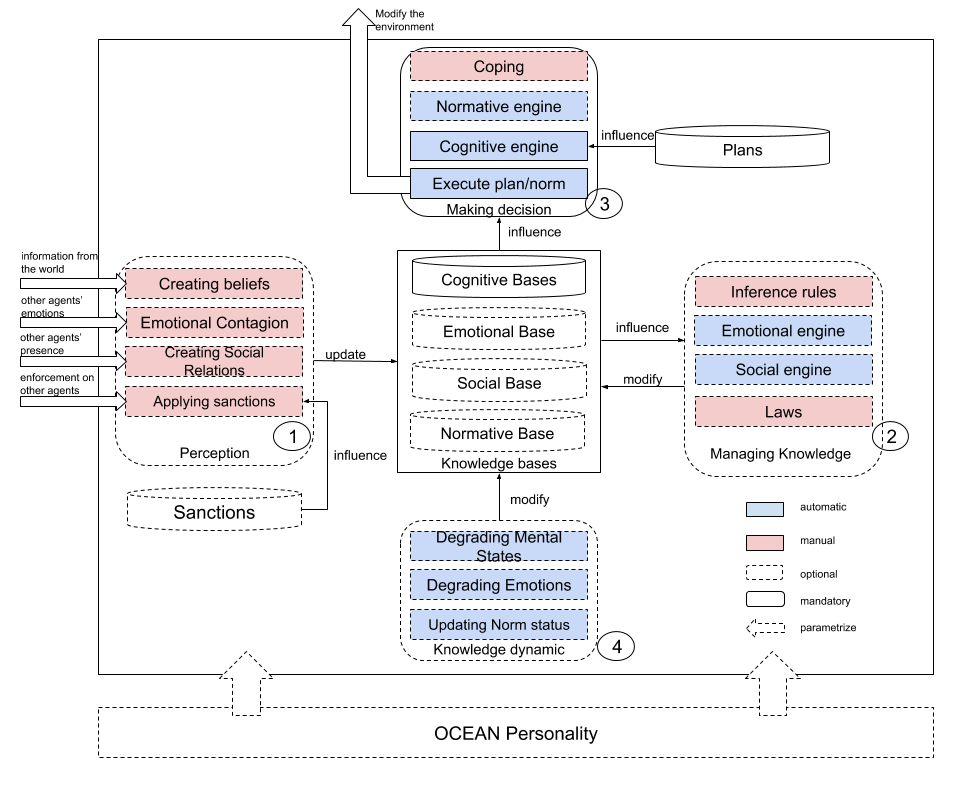
Each social agent has its own instance of the BEN architecture to make a decision. The architecture is composed of 4 main parts connected to the agent's knowledge bases, seated on the agent's personnality. Each part is made up of processes that are automatically computed (in blue) or which need to be manually defined by the modeler (in pink). Some of these processes are mandatory (in solid line) and some others are optional (in dotted line). This modularity enables each modeler to only use components that seem pertinent to the studied situation without creating heavy and useless computations.

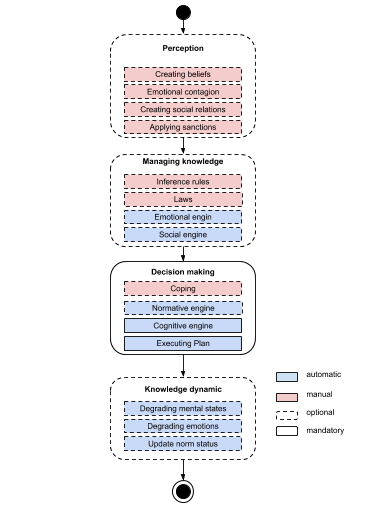
The Activity diagram bellow shows the order in which each module and each process is activated. The rest of this page explains in details how each process from each module works and what is the difference between the theoretical architecture and its implementation.

Predicates, knowledge and personality

In BEN, an agent represents its environment through the concept of predicates.

A predicate represents information about the world. This means it may represent a situation, an event or an action, depending on the context. As the goal is to create behaviors for agents in a social environment, that is to say taking actions performed by other agents into account with facts from the environment in the decision making process, an information P caused by an agent j with an associated list of value V is represented by P_j(V). A predicate P represents an information caused by any or none agent, with no particular value associated. The opposite of a predicate P is defined as not P.

In GAML, the simple_bdi architecture adds a new type called predicate which is made of a name (mandatory), a map of values (optional) an agent causing it (optional) and a truth value (optional, by default at true). To manipulate these predicates, there are operators like set_agent_cause, set_truth, with_values and add_values to modify the corresponding attribute of a given predicate (with_values changes all the map of values while add_values enables to add a new value without changing the rest of the map). These values can be accessed with operators get_agent_cause, get_truth, get_values. An operator not is also defined for predicates.

Below is an example of how to define predicates in GAML:

predicate a <- new_predicate("test");
predicate a <- new_predicate("test",["value1"::10]);
predicate b <- new_predicate("test",agentBob);
predicate c <- new_predicate("test",false);
predicate d <- new_predicate("test",agenBob,false);

Cognitive mental states

Through the architecture, an agent manipulates cognitive mental states to make a decision; they constitute the agent's mind. A cognitive mental state possessed by the agent $i$ is represented by M_i(PMEm,Val,Li) with the following meaning:

• M: the modality indicating the type of the cognitive mental state (e.g. a belief).
• PMEm: the object with which the cognitive mental state relates. It can be a predicate, another cognitive mental state, or an emotion.
• Val: a real value which meaning depends on the modality.
• Li: a lifetime value indicating the time before the cognitive mental state is forgotten.

A cognitive mental state with no particular value and no particular lifetime is written M_i(PMEm). Val[M_i(PMEm)] represents the value attached to a particular cognitive mental state and Li[M_i(PMEm)] represents its lifetime.

The cognitive part of BEN is based on the BDI paradigm (Bratman, 1987) in which agents have a belief base, a desire base and an intention base to store the cognitive mental states about the world. In order to connect cognition with other social features, the architecture outlines a total of 6 different modalities which are defined as follows:

• Belief: represents what the agent knows about the world. The value attached to this mental state indicates the strength of the belief.
• Uncertainty: represents an uncertain information about the world. The value attached to this mental state indicates the importance of the uncertainty.
• Desire: represents a state of the world the agent wants to achieve. The value attached to this mental state indicates the priority of the desire.
• Intention: represents a state of the world the agent is committed to achieve. The value attached to this mental state indicates the priority of the intention.
• Ideal: represents an information socially judged by the agent. The value attached to this mental state indicates the praiseworthiness value of the ideal about P. It can be positive (the ideal about P is praiseworthy) or negative (the ideal about P is blameworthy).
• Obligation: represents a state of the world the agent has to achieve. The value attached to this mental state indicates the priority of the obligation.

In GAML, mental states are manipulated thanks to add, remove and get actions related to each modality: add_belief, remove_belief, get_belief, add_desire, remove_desire ... Then, operators enables to acces or modify each attribute of a given mental state: get_predicate, set_predicate, get_strength, set_strength, get_lifetime, set_lifetime, etc.

Below is an exemple of code in GAML concerning cognitive mental states:

reflex testCognition{
    predicate a <- new_predicate("test");
    do add_belief(a,strength1,lifetime1);
    mental_state b <- get_uncertainty(a);
    int c <- get_lifetime(b);
}

Emotions

In BEN, the definition of emotions is based on the OCC theory of emotions (Ortony, 90). According to this theory, an emotion is a valued answer to the appraisal of a situation. Once again, as the agents are taken into consideration in the context of a society and should act depending on it, the definition of an emotion needs to contain the agent causing it. Thus, an emotion is represented by Em_i(P,Ag,I,De) with the following elements :

• Em_i: the name of the emotion felt by agent i.
• P: the predicate representing the fact about which the emotion is expressed.
• Ag: the agent causing the emotion.
• I: the intensity of the emotion.
• De: the decay withdrawal from the emotion's intensity at each time step.

An emotion with any intensity and any decay is represented by Em_i(P,Ag) and an emotion caused by any agent is written Em_i(P). I[Em_i(P,Ag)] stands for the intensity of a particular emotion and De[Em_i(P,Ag)] stands for its decay value.

In GAML, emotions are manipulated thanks to add_emotion, remove_emotion and get_emotion actions and attributes of an emotion are manipulated with set and get operators (set_intensity, set_about, set_decay, set_agent_cause, get_intensity, get_about, get_decay, get_agent_cause).

Below is an exemple of code in GAML concerning cognitive mental states:

reflex testEmotion{
    predicate a <- new_predicate("test");
    do add_emotion("hope",a);
    do add_emotion("joy",a,intesity1,decay1);
    float c <- get_intensity(get_emotion(new_emotion("joy",a)));
}

Social relations

As people create social relations when living with other people and change their behavior based on these relationships, BEN architecture makes it possible to describe social relations in order to use them in agents' behavior. Based on the research carried out by (Svennevig, 2000), a social relation is described by using a finite set of variables. Svennevig identifies a minimal set of four variables: liking, dominance, solidarity, and familiarity. A trust variable is added to interact with the enforcement of social norms. Therefore, in BEN, a social relation between agent i and agent j is expressed as R_i,j(L,D,S,F,T) with the following elements:

• R: the identifier of the social relation.
• L: a real value between -1 and 1 representing the degree of liking with the agent concerned by the link. A value of -1 indicates that agent j is hated, a value of 1 indicates that agent j is liked.
• D: a real value between -1 and 1 representing the degree of power exerted on the agent concerned by the link. A value of -1 indicates that agent j is dominating, a value of 1 indicates that agent j is dominated.
• S: a real value between 0 and 1 representing the degree of solidarity with the agent concerned by the link. A value of 0 indicates that there is no solidarity with agent j, a value of 1 indicates a complete solidarity with agent j.
• F: a real value between 0 and 1 representing the degree of familiarity with the agent concerned by the link. A value of 0 indicates that there is no familiarity with agent j, a value of 1 indicates a complete familiarity with agent j.
• T: a real value between -1 and 1 representing the degree of trust with the agent j. A value of -1 indicates doubts about agent j while a value of 1 indicates complete trust with agent j. The trust value does not evolve automatically in accordance with emotions.

With this definition, a social relation is not necessarily symmetric, which means R_i,j(L,D,S,F,T) is not equal by definition to R_i,j(L,D,S,F,T). L[R_i,j] stands for the liking value of the social relation between agent i and agent j, D[_i,j] stands for its dominance value, S[R_i,j] for its solidarity value, F[R_i,j] represents its familiarity value and T[R_i,j] its trust value.

In GAML, social relations are manipulated with add_social_link, remove_social_link and get_social_link actions. Each feature of a social link is accessible with set and gt operators (set_agent, get_agent, set_liking, get_liking, set_dominance, etc.)

Below is an exemple of code to manipulates social relations in GAML:

reflex testSocialRelations{
    do add_social_relation(new_social_relation(agentAlice));
    do add_social_relation(new_social_relation(agentBob,0.5,-0.3,0.2,0.1,0.8));
    float a <- get_liking(get_social_relation(new_social_relation(agentBob)));
    set_dominance(get_social_relation(new_social_relation(agentBob)),0.3);
}

Personality and additionnal variables

In order to define personality traits, BEN relies on the OCEAN model (McCrae, 1992), also known as the big five factors model. In the BEN architecture, this model is represented through a vector of five values between 0 and 1, with 0.5 as the neutral value. The five personality traits are:

• O: represents the openness of someone. A value of 0 stands for someone narrow-minded, a value of 1 stands for someone open-minded.
• C: represents the consciousness of someone. A value of 0 stands for someone impulsive, a value of 1 stands for someone who acts with preparations.
• E: represents the extroversion of someone. A value of 0 stands for someone shy, a value of 1 stands for someone extrovert.
• A: represents the agreeableness of someone. A value of 0 stands for someone hostile, a value of 1 stands for someone friendly.
• N: represents the degree of control someone has on his/her emotions, called neurotism. A value of 0 stands for someones neurotic, a value of 1 stands for someone calm.

In GAML, these variables are build-in attributes of agents using the simple_bdi control architecture. They are called openness, conscientiousness, extroversion, agreeableness and neurotism. To use this personality to automaticaly parametrize the other modules, a modeler needs to indicate it as shown in the GAML example below:

species miner control:simple_bdi {
    ...
    bool use_personality <- true;
    float openness <- 0.1;
    float conscientiousness <- 0.2;
    float extroversion <- 0.3;
    float agreeableness <- 0.4;
    float neurotism <- 0.5;
    ...
}

With BEN, the agent has variables related to some of the social features. The idea behind the BEN architecture is to connect these variables to the personality module and in particular to the five dimensions of the OCEAN model in order to reduce the number of parameters which need to be entered by the user. These additional variables are:

• The probability to keep the current plan.
• The probability to keep the current intention.
• A charisma value linked to the emotional contagion process.
• An emotional receptivity value linked to the emotional contagion.
• An obedience value used by the normative engine.

With the cognition, the agent has two parameters representing the probability to randomly remove the current plan or the current intention in order to check whether there could be a better plan or a better intention in the current context. These two values are connected to the consciousness components of the OCEAN model as it describes the tendency of the agent to prepare its actions (with a high value) or act impulsively (with a low value).

• Probability Keeping Plans = C^1/2
• Probability Keeping Intentions = C^1/2

For the emotional contagion, the process (presented later) requires charisma (Ch) and emotional receptivity (R) to be defined for each agent. In BEN, charisma is related to the capacity of expression, which is related to the extroversion of the OCEAN model, while the emotional receptivity is related to the capacity to control the emotions, which is expressed with the neurotism value of OCEAN.

• Ch = E
• R = 1 - N

With the concept of norms, the agent has a value of obedience between 0 and 1, which indicates its tendency to follow laws, obligations, and norms. According to research in psychology, which tried to explain the behavior of people participating in a recreation of the Milgram's experiment (Begue, 2015), obedience is linked with the notions of consciousness and agreeableness which gives the following equation:

• obedience = ((C+A)/2)^1/2

With the same idea, all the parameters required by each process are linked to the OCEAN model.

If a modeler wants to put a different value to one of these variables, he/she just need to indicate a new value manualy. For the probability to keep the current plan and the probability to keep the current intention, he/she also has to indicates it with a particular boolean value, as shown in the GAML example below:

species miner control: simple_bdi {
    ...
    bool use_personality <- true;
    bool use_persistence <- true;
    float plan_persistence <- 0.3;
    float intention_persistence <- 0.4;
    float obedience <- 0.2;
    float charisma <- 0.3
    float receptivity <- 0.6;
    ...
}

Perception

The first step of BEN is the perception of the environment. This module is used to connect the environment to the knowledge of the agent, transforming information from the world into cognitive mental states, emotions or social links but also used to apply sanctions during the enforcement of norms from other agents.

Below is an example of code to define a perception in GAML:

perceive target: fireArea in: 10{
    ...
}

The first process in this perception consists of adding beliefs about the world. During this phase, information from the environment is transformed into predicates which are included in beliefs or uncertainties and then added to the agent's knowledge bases. This process enables the agent to update its knowledge about the world. From the modeler's point of view, it is only necessary to specify which information is transformed into which predicate. The addition of a belief Belief_A(X) triggers multiple processes :

• it removes Belief_A(not X).
• it removes Intention_A(X).
• it removes Desire_A(X) if Intention_A(X) has just been removed.
• it removes Uncertainty_A(X) or Uncertainty_A(not X).
• it removes Obligation_A(X). \end{itemize}

In GAML, the focus statement eases the use of this process. Below is an example that adds a belief and an uncertainty with the focus statement during a perception:

perceive target: fireArea in: 10{
    focus id:"fireLocation" var:location strength:10.0;
    //is equivalent to ask myself {do add_belief(new_predicate("fireLocation",["location_value"::myself.location],10.0);}
    focus id:"hazardLocation" var:location strength:1.0 is_uncertain:true;
    //is equivalent to ask myself {do add_uncertainty(new_predicate("hazardLocation",["location_value"::myself.location],1.0);}
}

The emotional contagion enables the agent to update its emotions according to the emotions of other agents perceived. The modeler has to indicate the emotion triggering the contagion, the emotion created in the perceiving agent and the threshold of this contagion; the charisma (Ch) and receptivity (R) values are automatically computed as explained previously. The contagion from agent i to agent j occurs only if Ch_i x R_j is superior or equal to the threshold, which value is 0.25 by default. Then, the presence of the trigger emotion in the perceived agent is checked in order to create the emotion indicated.

The intensity and decay value of the emotion acquired by contagion are automatically computed.

• If Em_j(P) already exists:
  • I[Em_j(P)] = I[Em_j(P)] + I[Em_i(P)] x Ch_i x R_j
  • if pEm_i(P)] > I[Em_j(P)]:
    • De[Em_j(P)] = De[Em_i(P)]
  • if I[Em_j(P)] > I[Em_i(P)]:
    • De[Em_j(P)] = De[Em_j(P)]
• If Em_j(P) does not already exist:
  • I[Em_j(P)] = I[Em_i(P)] x Ch_i x R_j
  • De[Em_j(P)] = De[Em_i(P)].

In GAML, emotional_contagion statement helps to define an emotional contagion during a perception, as shown below:

perceive target: otherHumanAgents in: 10{
    emotional_contagion emotion_detected:fearFire threshold:contagionThreshold;
    //creates the detected emotion, if detected, in the agent doing the perception.
    emotional_contagion emotion_detected:joyDance emotion_created:joyPartying;
    //creates the emotion "joyPartying", if emotion "joyDance" is detected in the perceived agent.
}

During the perception, the agent has the possibility of creating social relations with other perceived agents. The modeler indicates the initial value for each component of the social link, as explained previously. By default, a neutral relation is created, with each value of the link at 0.0. Social relations can also be defined before the start of the simulation, to indicate that an agent has links with other agents at the start of the simulation, like links with friends or family members.

In GAML, the socialize statement help creating dynamicaly new social relations, as shown below:

perceive target:otherHumanAgents in: 10{
    socialize;
    //creates a neutral relation
    socialize dominance: -0.8 familiarity:0.2 when: isBoss;
    //example of a social link with precise values for some of its dimensions in a certain context
}

Finally, the agent may apply sanctions through the norm enforcement of other agents perceived. The modeler needs to indicate which modality is enforced and the sanction and reward used in the process. Then, the agent checks if the norm, the obligation, or the law, is violated, applied or not activated by the perceived agent. Notions of norms laws and obligations and how they work are explained later in this ocument.

A norm is considered violated when its context is verified, and yet the agent chose another norm or another plan to execute because it decided to disobey. A law is considered violated when its context is verified, but the agent disobeyed it, not creating the corresponding obligation. Finally, an obligation is considered violated if the agent did not execute the corresponding norm because it chose to disobey.

Below is an example of how to define an enforcement in GAML:

species miner skills: [moving] control:simple_bdi {
    ...
    perceive target: miner in: viewdist {
	myself.agent_perceived<-self;
	enforcement norm:"share_information" sanction:"sanctionToNorm" reward:"rewardToNorm";
    }
		
    sanction sanctionToNorm{
	do change_liking(agent_perceived,-0.1);
    }	
	
    sanction rewardToNorm{
	do change_liking(agent_perceived,0.1);
    }
}

Managing knowledge bases

The second step of the architecture, corresponding to the module number 2, consists of managing the agent's knowledge. This means updating the knowledge bases according to the latest perceptions, adding new desires, new obligations, new emotions or updating social relations, for example.

Modelers have to use inference rules for this purpose. Theses rules are triggered by a new belief, a new uncertainty or a new emotion, in a certain context, and may add or remove any cognitive mental state or emotion indicated by the user. Using multiple inference rules helps the agent to adapt its mind to the situation perceived without removing all its older cognitive mental states or emotions, thus enabling the creation of a cognitive behavior. These inference rules enable to link manually the various dimensions of an agent, for example creating desires depending on emotions, social relations and personality.

In GAML, the rule statement enables to define inference rules:

species miner skills: [moving] control: simple_bdi {
    ...
    perceive target: miner in: viewdist {
	...
    }
    ...
    rule belief: new_predicate("testA") new_desire: new_predicate("testB");
}

Using the same idea, modelers can define laws. These laws enable the creation of obligations in a given context based on the newest beliefs created by the agent through its perception or its inference rules. The modeler also needs to indicate an obedience threshold and if the agent's obedience value is below that threshold, the law is violated. If the law is activated, the obligation is added to the agent's cognitive mental state bases. The definition of laws makes it possible to create a behavior based on obligations imposed upon the agent.

Below is an example of the definition of a law statement in GAML:

law belief: new_predicate("testA") new_obligation:new_predicate("testB") threshold:thresholdLaw;

Emotional engine

BEN enables the agent to get emotions about its cognitive mental states. This addition of emotions is based on the OCC model (Ortony, 1990) and its logical formalism (Adam, 2007), which has been proposed to integrate the OCC model in a BDI formalism.

According to the OCC theory, emotions can be split into three groups: emotions linked to events, emotions linked to people and actions performed by people, and emotions linked to objects. In BEN, as the focus is on relations between social agents, only the first two groups of emotions (emotions linked to events and people) are considered.

The twenty emotions defined in this paper can be divided into seven groups depending on their relations with mental states: emotions about beliefs, emotions about uncertainties, combined emotions about uncertainties, emotions about other agents with a positive liking value, emotions about other agents with a negative liking value, emotions about ideals and combined emotions about ideals. All the initial intensities and decay value are computed using the OCEAN model and the value attached to the concerned mental states.

The emotions about beliefs are joy and sadness and are expressed this way:

• Joy_i(P_j,j) = Belief_i(P_j) & Desire_i(P)

• Sadness_i(P_j,j) = Belief_i(P_j) & Desire_i(not P)

Their initial intensity is computed according to the following equation with N the neurotism component from the OCEAN model:

• I[Em_i(P)] = V[Belief_i(P)] x V[Desire_i(P)] x (1+(0,5-N))

The emotions about uncertainties are fear and hope and are defined this way:

• Hope_i(P_j,j) = Uncertainty_i(P_j) & Desire_i(P)
• Fear_i(P_j,j) = Uncertainty_i(P_j) & Desire_i(not P)

Their initial intensity is computed according to the following equation:

• I[Em_i(P)] = V[Uncertainty_i(P)] x V[Desire_i(P)] x (1+(0,5-N))

Combined emotions about uncertainties are emotions built upon fear and hope. They appear when an uncertainty is replaced by a belief, transforming fear and hope into satisfaction, disappointment, relief or fear confirmed and they are defined this way:

• Satisfaction_i(P_j,j) = Hope_i(P_j,j) & Belief_i(P_j)
• Disappointment_i(P_j,j) = Hope_i(P_j,j) & Belief_i(not P_j)
• Relief_i(P_j,j) = Fear_i(P_j,j) & Belief_i(not P_j)
• Fear confirmed_i(P_j,j) = Fear_i(P_j,j) & Belief_i(P_j)

Their initial intensity is computed according to the following equation with Em'_i(P) the emotion of fear/hope.

• I[Em_i(P)] = V[Belief_i(P)] x I[Em'_i(P)]

On top of that, according to the logical formalism (Adam, 2007), four inference rules are triggered by these emotions:

• The creation of fear confirmed or the creation of relief will replace the emotion of fear.
• The creation of satisfaction or the creation of disappointment will replace a hope emotion.
• The creation of satisfaction or relief leads to the creation of joy.
• The creation of disappointment or fear confirmed leads to the creation of sadness.

The emotions about other agents with a positive liking value are emotions related to emotions of other agents which are in a the social relation base with a positive liking value on that link. They are the emotions called "happy for" and "sorry for" which are defined this way :

• Happy for_i(P,j) = L[R_i,j]>0 & Joy_j(P)
• Sorry for_i(P,j) = L[R_i,j]>0 & Sadness_j(P)

Their initial intensity is computed according to the following equation with A the agreeableness value from the OCEAN model.

• I[Em_i(P)] = I[Em_j(P)] x L[R_i,j] x (1-(0,5-A))

Emotions about other agents with a negative liking value are close to the previous definitions, however, they are related to the emotions of other agents which are in the social relation base with a negative liking value. These emotions are resentment and gloating and have the following definition:

• Resentment_i(P,j) = L[R_i,j]<0 & Joy_j(P)
• Gloating_i(P,j) = L[R_i,j]<0 & Sadness_j(P)

Their initial intensity is computed according to the following equation. This equation can be seen as the inverse of Equation \eqref{eqIntensEmo4}, and means that the intensity of resentment or gloating is greater if the agent has a low level of agreeableness contrary to the intensity of "happy for" and "sorry for".

• I[Em_i(P)] = I[Em_j(P)] x |L[R_i,j]| x (1+(0,5-A))

Emotions about ideals are related to the agent's ideal base which contains, at the start of the simulation, all the actions about which the agent has a praiseworthiness value to give. These ideals can be praiseworthy (their praiseworthiness value is positive) or blameworthy (their praiseworthiness value is negative). The emotions coming from these ideals are pride, shame, admiration and reproach and have the following definition:

• Pride_i(P_i,i) = Belief_i(P_i) & Ideal_i(P_i) & V[Ideal_i(P_i)]>0
• Shame_i(P_i,i) = Belief_i(P_i) & Ideal_i(P_i) & V[Ideal_i(P_i)]<0
• Admiration_i(P_j,j) = Belief_i(P_j) & Ideal_i(P_j) & V[Ideal_i(P_j)]>0
• Reproach_i(P_j,j) = Belief_i(P_j) & Ideal_i(P_j) & V[Ideal_i(P_j)]<0

Their initial intensity is computed according to the following equation with O the openness value from the OCEAN model:

• I[Em_i(P)] = V[Belief_i(P)] x |V[Ideal_i(P)]| x (1+(0,5-O))

Finally, combined emotions about ideals are emotions built upon pride, shame, admiration and reproach. They appear when joy or sadness appear with an emotion about ideals. They are gratification, remorse, gratitude and anger which are defined as follows:

• Gratification_i(P_i,i) = Pride_i(P_i,i) & Joy_i(P_i)
• Remorse_i(P_i,i) = Shame_i(P_i,i) & Sadness_i(P_i)
• Gratitude_i(P_j,j) = Admiration_i(P_j,j) & Joy_i(P_j)
• Anger_i(P_j,j) = Reproach_i(P_j,j) & Sadness_i(P_j)

Their initial intensity is computed according to the following equation with Em'_i(P) the emotion about ideals and Em"_i(P) the emotion about beliefs.

• I[Em_i(P)] = I[Em'_i(P)] x I[Em"_i(P)]

In order to keep the initial intensity of each emotion between 0 and 1, each equation is truncated between 0 an 1 if necessary.

The initial decay value for each of these twenty emotions is computed according to the same equation with D_eltat a time step which enables to define that an emotion does not last more than a given time:

• De[Em_i(P)] = N x I[Em_i(P)] x D_eltat

To use this automatic computation of emotion, a modeler need to activate it as shown in the GAML example below :

species miner control:simple_bdi {
    ...
    bool use_emotions_architecture <- true;
    ...
}

Social Engine

When an agent already known is perceived (i.e. there is already a social link with it), the social relationship with this agent is updated automatically by BEN. This update is based on the work of (Ochs, 2009) and takes the agent's cognitive mental states and emotions into account. In this section, the automatic update of each variable of a social link R_i,j(L,D,S,F,T) by the architecture is described in details; the trust variable of the link is however not updated automatically.

• Liking: according to (Ortony, 1991), the degree of liking between two agents depends on the valence (positive or negative) of the emotions induced by the corresponding agent. In the emotional model of the architecture, joy and hope are considered as positive emotions (satisfaction and relief automatically raise joy with the emotional engine) while sadness and fear are considered as negative emotions (fear confirmed and disappointment automatically raise sadness with the emotional engine). So, if an agent i has a positive (resp. negative) emotion caused by an agent j, this will increase (resp. decrease) the value of appreciation in the social link from i concerning j.

Moreover, research has shown that the degree of liking is influenced by the solidarity value \cite{smith2014social}. This may be explained by the fact that people tend to appreciate people similar to them.

The computation formula is described with the following equation with mPos the mean value of all positive emotions caused by agent j, mNeg the mean value of all negative emotions caused by agent j and a_L a coefficient depending of the agent's personality, indicating the importance of emotions in the process, and which is described below.

• L[R_i,j]=L[R_i,j]+|L[R_i,j]|(1-|L[R_i,j]|)S[R_i,j] + a_L (1-|L[R_i,j]|)(mPos-mNeg)

• a_L = 1-N

• Dominance : (Keltner, 2001) and (Shiota, 2004) explain that an emotion of fear or sadness caused by another agent represent an inferior status. But (Knutson, 1996) explains that perceiving fear and sadness in others increases the sensation of power over those persons.

The computation formula is described by the following equation with mSE the mean value of all negative emotions caused by agent i to agent j, mOE the mean value of all negative emotions caused by agent j to agent i and a_D a coefficient depending on the agent's personality, indicating the importance of emotions in the process.

• D[R_i,j]=D[R_i,j] + a_D (1-|D[R_i,j]|)(mSE-mOE)

• a_D = 1-N

• Solidarity: The solidarity represents the degree of similarity of desires, beliefs, and uncertainties between two agents. In BEN, the evolution of the solidarity value depends on the ratio of similarity between the desires, beliefs, and uncertainties of agent i and those of agent j. To compute the similarities and oppositions between agent i and agent j, agent i needs to have beliefs about agent j's cognitive mental states. Then it compares these cognitive mental states with its own to detect similar or opposite knowledge.

On top of that, negative emotions tend to decrease the value of solidarity between two people. The computation formula is described by the following equation with sim the number of cognitive mental states similar between agent i and agent j, opp the number of opposite cognitive mental states between agent i and agent j, NbKnow the number of cognitive mental states in common between agent i and agent j, mNeg the mean value of all negative emotions caused by agent j, a_S1 a coefficient depending of the agent's personality, indicating the importance of similarities and oppositions in the process, and a_S2 a coefficient depending of the agent's personality, indicating the importance of emotions in the process.

• S[R_i,j]=S[R_i,j] + S[R_i,j] x (1-S[R_i,j]) x (a_S1 (sim-opp)/(NbKnow) - a_S2 mNeg))

• a_S1 = 1-O

• a_S2 = 1-N

• Familiarity: In psychology, emotions and cognition do not seem to impact the familiarity. However, (Collins, 1994) explains that people tend to be more familiar with people whom they appreciate. This notion is modeled by basing the evolution of the familiarity value on the liking value between two agents. The computation formula is defined by the following equation.

• F[R_i,j]=F[R_i,j] x (1+L[R_i,j])

The trust value is not evolving automatically in BEN, as there is no clear and automatic link with cognition or emotions. However, this value can evolve manually, especially with sanctions and rewards to social norms where the modeler can indicate a modification of the trust value during the enforcement process.

To use this automatic update of social relations, a modeler need to activate it as shown in the GAML example below:

species miner control: simple_bdi {
    ...
    bool use_social_architecture <- true;
    ...
}

Making Decision

The third part of the architecture is the only one mandatory as it is where the agent makes a decision. A cognitive engine can be coupled with a normative engine to chose an intention and a plan to execute. The complete engine is summed up in the figure below:

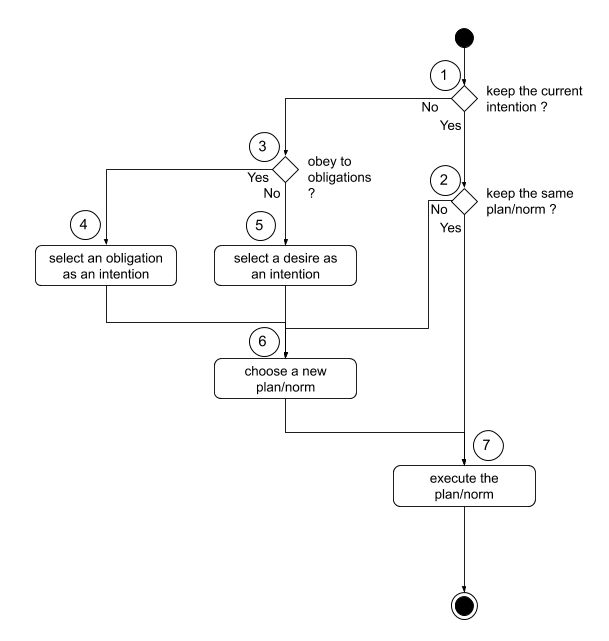
The decision-making process can be divided into seven steps:

• Step 1: the engine checks the current intention. If it is still valid, the intention is kept so the agent may continue to carry out its current plan.
• Step 2: the engine checks if the current plan/norm is still usable or not, depending on its context.
• Step 3: the engine checks if the agent obeys an obligation taken from the obligations corresponding to a norm with a valid context in the current situation and with a threshold level lower than the agent’s obedience value as computed in Section 4.1.
• Step 4: the obligation with the highest priority is taken as the current intention.
• Step 5: the desire with the highest priority is taken as the current intention.
• Step 6: the plan or norm with the highest priority is selected as the current plan/norm, among the plans or norms corresponding to the current intention with a valid context.
• Step 7: the behavior associated with the current plan/norm is executed.

Steps 4, 5 and 6 do not have to be deterministic; they may be probabilistic. In this case, the priority value associated with obligations, desires, plans, and norms serves as a probability.

In GAML, a modeler may indicate the use of a probabilistic or deterministic cognitive engine with the variable probabilistic_choice, as shown in the example code below:

species miner control: simple_bdi {
    ...
    bool probabilistic_choice <- true;
    ...
}

Defining plans

The modeler needs to define action plans which are used by the cognitive engine, as explained earlier. These plans are a set of behaviors executed in a certain context in response to an intention. In BEN, a plan owned by agent i is represented by Pl_i(Int,Cont,Pr,B) with:

• Pl: the name of the plan.
• Int: the intention triggering this plan.
• Cont: the context in which this plan may be applied.
• Pr: a priority value used to choose between multiple plans relevant at the same time. If two plans are relevant to the same priority, one is chosen at random.
• B: the behavior, as a sequence of instructions, to execute if the plan is chosen by the agent.

The context of a plan is a particular state of the world in which this plan should be considered by the agent making a decision. This feature enables to define multiple plans answering the same intention but activated in various contexts.

Below is an example for the definition of two plans answering the same intention in different contexts in GAML:

species miner control: simple_bdi {
    ...
    plan evacuationFast intention: in_shelter emotion: fearConfirmed priority:2 {
	color <- #yellow;
	speed <- 60 #km/#h;
	if (target = nil or noTarget) {
	    target <- (shelter with_min_of (each.location distance_to location)).location;
	    noTarget <- false;
	} else  {
	    do goto target: target on: road_network move_weights: current_weights recompute_path: false;
	    if (target = location)  {
		do die;
	    }		
	}
    }	
	
    plan evacuation intention: in_shelter finished_when: has_emotion(fearConfirmed){
	color <-#darkred;
	if (target = nil or noTarget) {
	    target <- (shelter with_min_of (each.location distance_to location)).location;
	    noTarget <- false;
	} else  {
	    do goto target: target on: road_network move_weights: current_weights recompute_path: false;
	    if (target = location)  {
		do die;
	    }		
	}
    }
    ...
}

Defining norms

A normative engine may be used within the cognitive engine, as it has been explained above. This normative engine means choosing an obligation as the current intention and selecting a set of actions to answer this intention. Also, the concept of social norms is modeled as a set of action answering an intention, which an agent could disobey.

In BEN, this concept of behavior which may be disobeyed is formally represented by a norm possessed by agent i No_i(Int,Cont,Ob,Pr,B,Vi) with:

• No: the name of the norm.
• Int: the intention which triggers this norm.
• Cont: the context in which this norm can be applied.
• Ob: an obedience value that serves as a threshold to determine whether or not the norm is applied depending on the agent's obedience value (if the agent's value is above the threshold, the norm may be executed).
• Pr: a priority value used to choose between multiple norms applicable at the same time.
• B: the behavior, as a sequence of instructions, to execute if the norm is followed by the agent.
• Vi: a violation time indicating how long the norm is considered violated once it has been violated.

In GAML, a norm is defined as follows:

species miner control: simple_bdi {
    ...
//this first norm answer an intention coming from an obligation
    norm doingJob obligation:has_gold finished_when: has_belief(has_gold) threshold:thresholdObligation{
        if (target = nil) {
	    do add_subintention(has_gold,choose_goldmine, true);
	    do current_intention_on_hold();
        } else {
	    do goto target: target ;
	    if (target = location)  {
		goldmine current_mine<- goldmine first_with (target = each.location);
		if current_mine.quantity > 0 {
		    gold_transported <- gold_transported+1;
	 	    do add_belief(has_gold);
		    ask current_mine {quantity <- quantity - 1;}	
		} else {
		    do add_belief(new_predicate(empty_mine_location, ["location_value"::target]));
		    do remove_belief(new_predicate(mine_at_location, ["location_value"::target]));
		}
		target <- nil;
	    }
	}	
    }

//this norm may be seen as a "social norm" as it answers an intention not coming from an obligation but may be disobeyed
    norm share_information intention:share_information threshold:thresholdNorm instantaneous: true{
	list<miner> my_friends <- list<miner>((social_link_base where (each.liking > 0)) collect each.agent);
	loop known_goldmine over: get_beliefs_with_name(mine_at_location) {
	    ask my_friends {
		do add_belief(known_goldmine);
	    }
	}
	loop known_empty_goldmine over: get_beliefs_with_name(empty_mine_location) {
	    ask my_friends {
		do add_belief(known_empty_goldmine);
	    }
	}
		
	do remove_intention(share_information, true); 
    }
    ...
}

Dynamic knowledge

The final part of the architecture is used to create a temporal dynamic to the agent's behavior, useful in a simulation context. To do so, this module automatically degrades mental states and emotions and updates the status of each norm.

The degradation of mental states consists of reducing their lifetime. When the lifetime is null, the mental state is removed from its base. The degradation of emotions consists of reducing the intensity of each emotion stored by its decay value. When the intensity of an emotion is null, the emotion is removed from the emotional base.

In GAML, if a mental state has a lifetime value or if an emotion has an intensity and a decay value, this degradation process is done automatically.

Finally, the status of each norm is updated to indicate if the norm was activated or not (if the context was right or wrong) and if it was violated or not (the norm was activated but the agent disobeyed it). Also, a norm can be violated for a certain time which is updated and if it becomes null, the norm is not violated anymore.

These last steps enable the agent's behavior's components to automatically evolve through time, leading the agents to forget a piece of knowledge after a certain amount of time, creating dynamics in their behavior.

Conclusion

The BEN architecture is already implemented in GAMA and may be accessed by adding the simple_bdi control architecture to the definition of a species.

A tutorial may be found with the BDI Tutorial.